Speculative Ensembles for Real-Time RF Classification

Introduction

In the world of edge RF (Radio Frequency) systems, balancing latency and accuracy is a constant challenge. A new approach called “speculative ensembles” offers a promising solution by combining fast and slow models to meet strict latency budgets while maintaining high accuracy.

The Concept

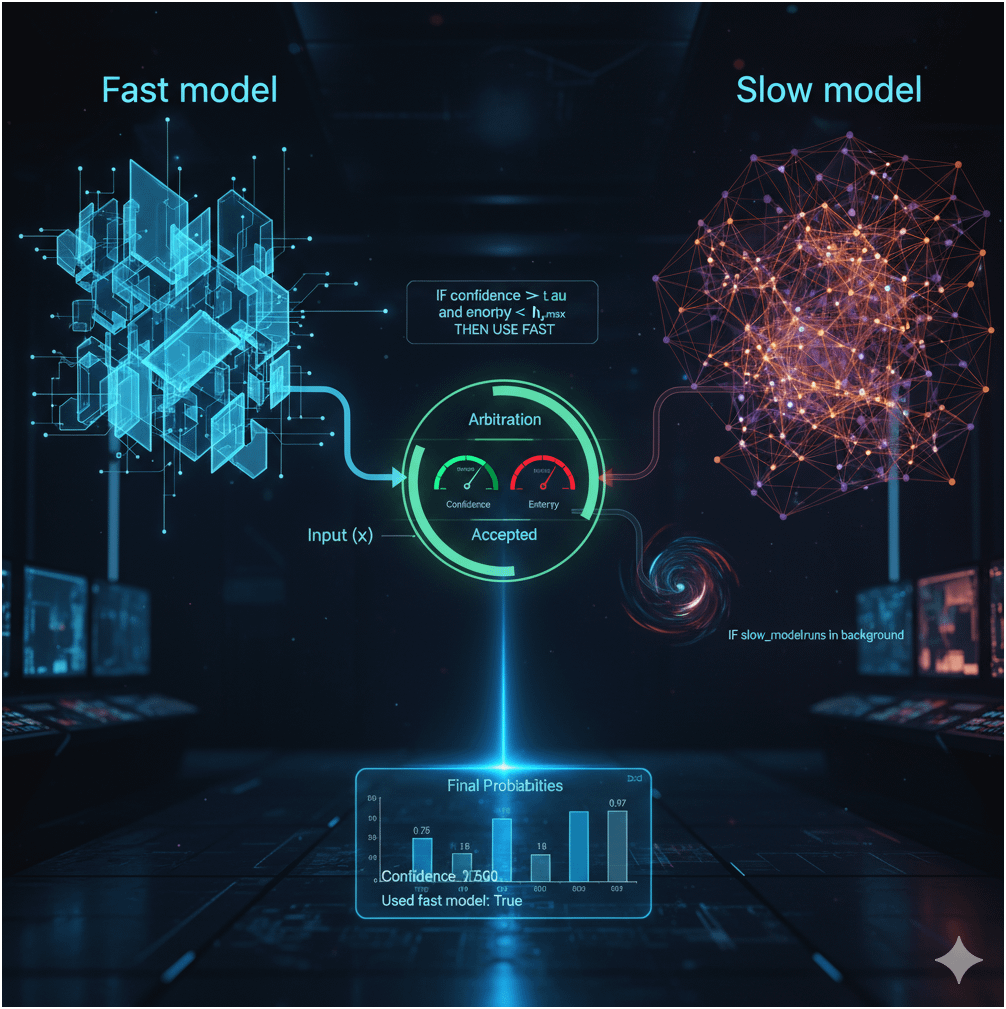
Speculative ensembles work by using a fast model to handle confident inputs and a slow model to arbitrate the rest. The fast model quickly processes straightforward cases, while uncertain ones are passed to the slow model for more thorough analysis. Predictions from both models are then fused using confidence-weighted probabilities to reduce bias.

Key Findings

• Under a 50 ms latency budget, the ensemble achieves 92.2% accuracy with a median latency of 26.0 ms, offering a 1.65× speed-up compared to the slow model alone (43.0 ms), while retaining most of its accuracy (92.8%).
• The system accepts 62% of inputs via the fast model, demonstrating efficient arbitration.
• An “anytime knob” allows tuning of the confidence threshold to trade off between accuracy and latency, providing flexibility for different operational needs.

How It Works

• Arbitration Rule: The fast model’s predictions are accepted if they meet a confidence threshold and have low entropy; otherwise, they are deferred to the slow model.
• Fusion: For accepted fast predictions, a weighted fusion with the slow model’s output (computed in the background) enhances accuracy.
• Calibration: Temperature scaling improves the reliability of confidence scores, ensuring robust decision-making.

Visual Insights

• Latency CDF: The ensemble’s median latency (26.0 ms) sits between the fast (18.5 ms) and slow (43.0 ms) models, showing a balanced performance.
• Acceptance Rate: Higher confidence thresholds reduce the percentage of cases handled by the fast model, allowing finer control.
• Reliability: Post-calibration, the accuracy aligns closely with confidence levels, reducing overconfidence.

Conclusion

This innovative approach leverages the strengths of both fast and slow models, offering a practical way to meet latency constraints without sacrificing accuracy. It’s a step forward for real-time RF classification, inspired by selective classification and speculative decoding techniques.

Speculative decoding is a technique inspired by the concept of generating a draft and then verifying it, commonly used in natural language processing to speed up inference in transformer models. In the context of the “Speculative Ensembles for Real-Time RF Classification” paper, it is adapted for radio frequency (RF) classification. Here’s how it works:

• The approach uses a fast model to quickly generate initial predictions (the “draft”) for RF inputs, accepting them when confidence is high (based on a confidence threshold and low entropy).
• Uncertain predictions are deferred to a slower, more accurate model (the “verifier”) that acts as an expert to refine or correct the draft.
• The final predictions are fused using confidence-weighted probabilities, combining the fast model’s output with the slow model’s verification to reduce bias and improve accuracy.

This method achieves a balance between speed and precision, attaining 92.2% accuracy with a median latency of 26.0 ms under a 50 ms budget—1.65× faster than the slow model alone (43.0 ms) while retaining most of its accuracy (92.8%). The technique leverages calibration (e.g., temperature scaling) to ensure reliable confidence scores, making it effective for real-time edge RF systems with strict latency constraints.

Temperature scaling is a calibration technique used to adjust the confidence scores of a model’s predictions, making them more reliable and aligned with actual accuracy. In the context of the “Speculative Ensembles for Real-Time RF Classification” paper, it plays a key role in improving the arbitration between fast and slow models.

How It Works

• A model’s raw output (logits) is converted to probabilities using a softmax function. Without adjustment, these probabilities can be overconfident, meaning the predicted confidence (e.g., 95%) may not match the true likelihood of being correct.
• Temperature scaling modifies the softmax by introducing a temperature parameter ( T ). The adjusted probability for class ( k ) is calculated as:
  [
  p_k = \frac{\exp(z_k / T)}{\sum_j \exp(z_j / T)}
  ]
  where ( z_k ) is the logit for class ( k ), and ( T ) is the temperature (typically ( T > 0 )).
• A ( T > 1 ) softens the distribution (lowers confidence), while ( T < 1 ) sharpens it (increases confidence). The optimal ( T ) is found using a held-out validation set to minimize the difference between predicted confidence and accuracy.

Application in the Paper

• The fast and slow models (a compact CNN/Transformer and a larger Transformer, respectively) are calibrated with temperature scaling to reduce overconfidence.
• This ensures that the confidence threshold ( \tau ) and entropy ( H(x) ) used in the arbitration rule (accept fast predictions if ( c(x) \geq \tau ) and ( H(x) \leq h )) are more trustworthy.
• Figure 4 (Reliability diagram) shows the effect: before scaling, confidence and accuracy diverge (e.g., 90% confidence might yield 70% accuracy); after scaling, the curve aligns closely with the diagonal, indicating well-calibrated predictions.

Benefits

• Improves the reliability of fast model acceptances, allowing more accurate deferral to the slow model when needed.
• Reduces Expected Calibration Error (ECE), enhancing the robustness of the speculative ensemble’s decision-making.
• Enables the “anytime knob” (sweeping ( \tau )) to effectively trade off latency and accuracy by ensuring confidence scores reflect true performance.

In summary, temperature scaling fine-tunes the confidence estimates, making the speculative ensemble’s fast/slow arbitration more effective under a 50 ms latency budget, achieving 92.2% accuracy with a 26.0 ms median latency.

Here’s a practical implementation example for the speculative ensembles approach described in the paper, written in Python. This example simulates the fast/slow arbitration and confidence-weighted fusion using a simplified setup.

import numpy as np
from scipy.special import softmax

# Simulated fast and slow model predictions (logits)
def fast_model(x):
    # Simple linear model as a stand-in for fast CNN/Transformer
    return np.array([2.0, 1.0, 0.5])  # Example logits

def slow_model(x):
    # More complex model as a stand-in for slow Transformer
    return np.array([2.2, 1.2, 0.6])  # Example logits

# Confidence and entropy calculation
def compute_confidence_entropy(logits):
    probs = softmax(logits)
    confidence = np.max(probs)  # Max probability
    entropy = -np.sum(probs * np.log(probs + 1e-10))  # Avoid log(0)
    return confidence, entropy

# Arbitration rule
def arbitrate(x, tau=0.9, h_max=1.0):
    fast_logits = fast_model(x)
    confidence, entropy = compute_confidence_entropy(fast_logits)
    if confidence >= tau and entropy <= h_max:
        return fast_logits, True  # Accept fast prediction
    return slow_model(x), False  # Defer to slow model

# Confidence-weighted fusion
def fuse_predictions(fast_probs, slow_probs, confidence, tau=0.9, gamma=10.0):
    alpha = 1.0 / (1.0 + np.exp(-gamma * (confidence - tau)))  # Sigmoid weighting
    return alpha * fast_probs + (1 - alpha) * slow_probs

# Main simulation
def run_speculative_ensemble(x):
    fast_logits, use_fast = arbitrate(x)
    fast_probs = softmax(fast_logits)
    confidence, _ = compute_confidence_entropy(fast_logits)
    
    if use_fast and False:  # Set to True if slow model runs in background
        slow_logits = slow_model(x)
        slow_probs = softmax(slow_logits)
        final_probs = fuse_predictions(fast_probs, slow_probs, confidence)
    else:
        final_probs = fast_probs
    
    return final_probs, confidence, use_fast

# Example usage
if __name__ == "__main__":
    x = np.random.rand(3)  # Dummy input
    probs, conf, used_fast = run_speculative_ensemble(x)
    print(f"Final probabilities: {probs}")
    print(f"Confidence: {conf:.3f}")
    print(f"Used fast model: {used_fast}")