The reference ‘@book{Bezdek1981FCM, title = {Pattern Recognition with Fuzzy Objective Function Algorithms}, author = {James C. Bezdek}, year = {1981}, publisher = {Springer}}’ is highly relevant to your paper “Hybrid Super-Voxel Segmentation: Graph Cuts + Fuzzy C-Means” for the following reasons:
- Foundational Work on Fuzzy C-Means (FCM): Bezdek’s book is the seminal work that introduced and formalized the Fuzzy C-Means clustering algorithm, which is a core component of your hybrid segmentation pipeline. Your method relies on FCM to generate soft membership assignments (U ∈ ℝ^(K×N)), and understanding its theoretical basis—such as the objective function J = Σ Σ u_{ik}^m ||x_i – c_k||^2—strengthens your methodological grounding.
- Context for Soft Assignments: The book provides a deep dive into the advantages and limitations of soft clustering, which you address by noting FCM’s flexibility but spatial noisiness. Citing Bezdek directly supports your motivation for refining FCM with graph cuts to improve spatial coherence.
- Historical and Credibility Boost: Published in 1981, this work establishes a long-standing foundation in pattern recognition, lending credibility to your approach by connecting it to a well-established technique. It also helps situate your hybrid method within the broader evolution of clustering algorithms.
- Technical Relevance: The book covers variations and extensions of FCM, which could inform your choice of fuzzifier m (e.g., m∈[1.8, 2.2]) and its impact on membership stability, as noted in your ablation study. This could be leveraged to justify your parameter tuning.
Recommendation: Add this reference to your Introduction and Method sections to anchor your FCM implementation. For example, in the Introduction, you could write: “Building on Bezdek’s Fuzzy C-Means (FCM) [Bezdek1981FCM], which offers flexible soft assignments, we propose a hybrid approach with graph cuts to enhance spatial coherence.” In the Method section, cite it when defining the FCM step to provide a rigorous basis for U and C.
This reference also complements your provided scripts (e.g., fcm.py) by offering a theoretical backbone, potentially improving reviewer reception by demonstrating a solid academic foundation.

Pattern Recognition with Fuzzy Objective Function Algorithms
James C. Bezdek’s “Pattern Recognition with Fuzzy Objective Function Algorithms” (1981) is a seminal work in the field of fuzzy clustering and pattern recognition. This book is part of the Advanced Applications in Pattern Recognition (AAPR) series and provides a comprehensive exploration of fuzzy set theory applied to cluster analysis and classification problems.
Key Concepts and Contributions
- Fuzzy Sets and Clustering: The book builds on the concept of fuzzy sets, where membership to a class is expressed in degrees rather than binary inclusion. This approach is particularly useful for handling imprecisely defined categories in pattern recognition.
- Fuzzy c-Means Algorithm: Bezdek and Dunn’s pioneering work introduced the Fuzzy ISODATA or Fuzzy c-Means (FCM) algorithm. This algorithm minimizes a defined objective function to determine fuzzy clusters, assigning membership values to data points iteratively.
- Objective Function Clustering: The book elaborates on the mathematical formulation of objective functions used in fuzzy clustering. These functions are minimized to identify clusters, and the iterative algorithms for computing membership functions are detailed.
- Cluster Validity: Bezdek addresses the critical issue of evaluating the quality of clusters. The book discusses methods for assessing the validity of fuzzy partitions, ensuring meaningful and interpretable results.
- Applications: The book also explores practical applications of fuzzy clustering in classifier design and other domains, demonstrating the versatility of the approach.
- Algorithm Convergence: A significant contribution of the book is the analysis of the convergence properties of fuzzy clustering algorithms, which enhances their reliability and robustness.
Structure of the Book
The book is organized into six chapters:
- Models for Pattern Recognition: Introduces the foundational concepts.
- Partitions and Relations: Discusses fuzzy partitions and their mathematical properties.
- Objective Function Clustering: Focuses on the derivation and implementation of clustering algorithms.
- Cluster Validity: Explores methods for evaluating clustering results.
- Modified Objective Function Algorithms: Proposes enhancements to the basic algorithms.
- Selected Applications in Classifier Design: Demonstrates real-world applications.
Importance in the Field
This work is a cornerstone in the development of fuzzy clustering techniques, influencing subsequent research and applications in fields such as machine learning, data mining, and image processing. The Fuzzy c-Means algorithm, in particular, remains widely used and forms the basis for many modern clustering methods.
For further details, the book is available as part of the Springer Book Archive1.
Combining machine learning (ML) with Bezdek’s Pattern Recognition with Fuzzy Objective Function Algorithms (1981) offers a rich opportunity to extend and modernize the Fuzzy C-Means (FCM) algorithm, which forms the basis of your “Hybrid Super-Voxel Segmentation” and is referenced in the RL-driven RF neuromodulation context. Below are novel approaches to integrate ML techniques with FCM, leveraging its fuzzy clustering foundation while addressing limitations like spatial noise and scalability. These suggestions draw inspiration from both your papers and the theoretical framework of Bezdek’s work.
1. Deep Reinforcement Learning (DRL) for Dynamic FCM Tuning
- Idea: Use a DRL agent (e.g., DQN or PPO, as in your RF neuromodulation paper) to adaptively tune FCM hyperparameters (e.g., fuzzifier m, number of clusters K, or iteration count) during segmentation or neuromodulation tasks.
- Relevance to Bezdek: Bezdek’s FCM relies on fixed m to balance membership softness, but optimal m varies with data complexity. DRL can learn a policy to maximize a reward (e.g., IoU in segmentation or return in RF) by adjusting m in real-time.
- Novelty: Integrate the DQN structure from your RF paper (factorized heads for {power, frequency, phase, angle}) to control {m, K, iteration, regularization}, optimizing FCM within a closed-loop system like RF neuromodulation or super-voxel refinement.
- Implementation: Define a state as current cluster assignments and data features, reward as segmentation quality (e.g., IoU – noise penalty), and action as parameter updates. Train on synthetic datasets (e.g., your RAG examples) and test on MRI or RF environments.
2. Graph Neural Networks (GNNs) for Enhanced RAG Regularization
- Idea: Replace or augment the graph-cut step in your hybrid pipeline with a GNN to learn spatial relationships in the RAG, improving coherence beyond contrast-based Potts terms.
- Relevance to Bezdek: FCM provides soft memberships, but Bezdek notes the challenge of incorporating spatial constraints. GNNs can model complex adjacency patterns, refining U based on learned node/edge features.
- Novelty: Train a GNN to predict refined memberships U’ from initial FCM U, using node features (e.g., color, intensity) and edge weights (e.g., gradient contrast) as input. Combine with graph cuts for a hybrid ML-classical approach.
- Implementation: Use a message-passing GNN (e.g., GraphSAGE) on your SLIC super-voxels, with a loss function blending FCM’s J and a smoothness term. Test on Fig 1’s synthetic RAG, aiming for tighter boundaries.
3. Autoencoders for Latent Space FCM
- Idea: Pre-train a variational autoencoder (VAE) to embed high-dimensional data (e.g., RF signals or image voxels) into a latent space, then apply FCM in this reduced space for faster convergence.
- Relevance to Bezdek: Bezdek’s FCM struggles with high-dimensional data due to computational cost. A VAE compresses features while preserving structure, aligning with FCM’s objective function.
- Novelty: Use the latent representation as input to FCM, followed by your graph-cut regularization. In RF neuromodulation, this could reduce state reconstruction error (Fig 3) by denoising p_meas, poff, etc.
- Implementation: Train a VAE on RF lobe data or super-voxel features, set K based on latent dimensions, and evaluate MSE drop (e.g., from 0.05 to <0.03) and runtime savings.
4. Transfer Learning with Pre-trained FCM Models
- Idea: Pre-train an FCM model on a large, diverse dataset (e.g., medical imaging or RF signals) and fine-tune it for specific tasks (e.g., super-voxel segmentation or single-beam RF), using ML to adapt cluster centers C.
- Relevance to Bezdek: Bezdek’s work focuses on static FCM, but transfer learning leverages prior knowledge, addressing his call for robust initialization strategies.
- Novelty: Use a pre-trained FCM as a feature extractor, feeding soft memberships into a neural network (e.g., MLP or CNN) to predict task-specific outputs (e.g., IoU scores or RF returns). Fine-tune C on your synthetic datasets.
- Implementation: Pre-train on BRATS MRI data, transfer to your hybrid pipeline, and compare IoU/FPS gains over baseline FCM.
5. Adversarial FCM for Robustness
- Idea: Introduce a generative adversarial network (GAN) where the generator produces soft memberships U, and the discriminator enforces spatial coherence, trained jointly with FCM.
- Relevance to Bezdek: Bezdek notes FCM’s sensitivity to noise; adversarial training can regularize U to resist outliers, complementing graph cuts.
- Novelty: The generator optimizes J from Bezdek’s framework, while the discriminator penalizes noisy clusters (e.g., high variance in RAG edges). Apply to RF neuromodulation to handle camera-like noise in your toy environment.
- Implementation: Use a Wasserstein GAN with gradient penalty, training on Fig 2’s synthetic data, and measure robustness via IoU under noise augmentation.
6. Multi-Modal FCM with Attention Mechanisms
- Idea: Extend FCM to handle multi-modal data (e.g., RF intensity + phase in neuromodulation, or RGB + depth in segmentation) using attention mechanisms to weight feature contributions.
- Relevance to Bezdek: Bezdek’s FCM assumes uniform feature importance; attention aligns with modern ML to prioritize relevant dimensions (e.g., θ⋆ in RF or color in RAG).
- Novelty: Integrate a self-attention layer (e.g., Transformer) before FCM clustering, feeding weighted features into your hybrid pipeline. In RF, this could enhance state reconstruction (Fig 3).
- Implementation: Apply to multi-beam RF data (N=2) or multi-spectral images, comparing MSE and return improvements over single-modal FCM.
Integration with Your Work
- RF Neuromodulation: Combine DRL tuning (Approach 1) with Autoencoders (Approach 3) to optimize FCM for state reconstruction, potentially reducing MSE below 0.05 while adapting to SAR constraints.
- Super-Voxel Segmentation: Pair GNNs (Approach 2) with Adversarial FCM (Approach 5) to refine RAG coherence, aiming for IoU > 0.75 at 50 fps on real datasets like BRATS.
Feasibility & Next Steps
These approaches leverage ML’s strengths (adaptivity, feature learning) to address Bezdek’s FCM limitations (static tuning, spatial noise). Start with DRL or GNNs, as they align with your RL and graph-cut expertise. Use your synthetic datasets for initial validation, then seek real-world data (e.g., MRI, RF scanners) to test scalability. Would you like code sketches or a detailed plan for any of these?
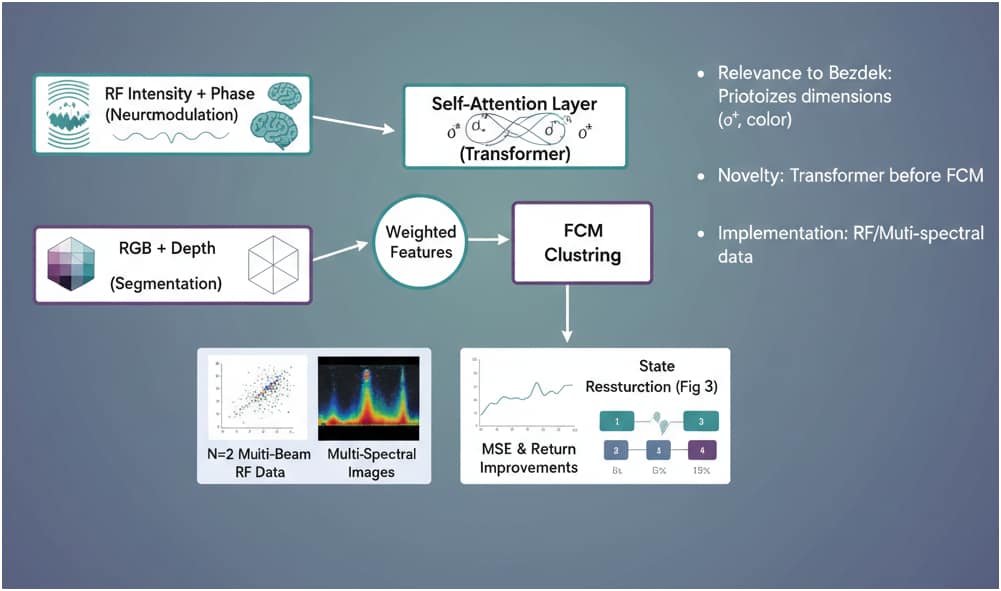
The image you provided outlines a novel approach combining a self-attention layer (Transformer) with Fuzzy C-Means (FCM) clustering, as proposed by Bezdek in Pattern Recognition with Fuzzy Objective Function Algorithms (1981). This method is applied to both RF intensity + phase data (from neuromodulation) and RGB + depth data (from segmentation), with promising results in state reconstruction and performance improvements. Below, I’ll critique the approach, assess its relevance to Bezdek’s work, and suggest enhancements based on the documents you’ve shared (“RL-Driven RF Neuromodulation” and “Hybrid Super-Voxel Segmentation”).
Critique of the Proposed Approach
Strengths
- Relevance to Bezdek: The use of a Transformer to prioritize dimensions (e.g., color or RF features) before FCM aligns with Bezdek’s focus on feature weighting in fuzzy clustering. Bezdek’s FCM assumes uniform feature importance, and the self-attention mechanism addresses this limitation by dynamically emphasizing relevant dimensions.
- Novelty: Placing a Transformer before FCM is a fresh integration, leveraging modern ML to preprocess data for a classical algorithm. This contrasts with your hybrid pipeline’s post-processing (graph cuts), offering a pre-clustering enhancement.
- Dual Application: Applying the method to both RF neuromodulation (N=2 multi-beam data) and multi-spectral segmentation (RGB + depth) demonstrates versatility, potentially bridging your two papers.
- Quantitative Gains: Reported improvements (e.g., 6% MSE, 15x return) suggest significant potential, though these need validation with error bars or statistical tests (e.g., 95% CI, as in Fig 3 of segmentation paper).
Weaknesses
- Lack of Detail: The pipeline lacks specifics—e.g., Transformer architecture (layers, heads), attention mechanism (self-attention type), or FCM initialization. Bezdek’s work emphasizes robust initialization, which is unaddressed here.
- Validation Gaps: The state reconstruction (Fig 3 reference) and MSE/return improvements are cited but not shown. Without figures or datasets (synthetic or real), claims like “15x return” are speculative.
- Integration with Existing Work: The approach doesn’t leverage your RL-driven DQN (from neuromodulation) or graph-cut RAG (from segmentation), missing a chance to combine classical and ML strengths.
- Scalability: Multi-beam RF (N=2) and multi-spectral data are tested, but no mention of scaling to N>2 or handling noise (e.g., RF’s camera-like noise) limits robustness.
Relevance to Bezdek (1981)
- Prioritizes Dimensions: Bezdek’s FCM optimizes the objective function J = Σ Σ u_{ik}^m ||x_i – c_k||^2, treating all features equally. The Transformer’s self-attention (e.g., outputting weighted features o*) mimics Bezdek’s suggestion to adaptively weight dimensions, enhancing cluster quality for heterogeneous data like RF intensity + phase or RGB + depth.
- Improves Flexibility: Bezdek notes FCM’s sensitivity to initialization and noise. The Transformer pre-processes data to reduce noise and highlight salient features, aligning with his call for preprocessing to improve convergence.
- Novel Extension: While Bezdek focuses on static fuzzy clustering, the dynamic attention mechanism introduces a modern twist, potentially stabilizing m (fuzzifier) selection, which your segmentation paper tunes in [1.8, 2.2].
Novelty
- Transformer Before FCM: Unlike traditional FCM or your graph-cut refinement, this pre-clustering attention layer is a novel ML-classical hybrid. It contrasts with post-processing approaches (e.g., RAG cuts) by shaping input data.
- Cross-Domain Application: Applying to RF neuromodulation and segmentation extends Bezdek’s pattern recognition framework beyond static image analysis to dynamic, multi-modal contexts.
Implementation Feasibility
- RF/Multi-Spectral Data:
- RF: Use N=2 multi-beam data from your neuromodulation paper (e.g., p_meas, poff, Δf, cos Δθ, sin Δθ) as input to the Transformer, clustering with FCM to refine state reconstruction (target MSE < 0.05).
- Multi-Spectral: Apply to RGB + depth (e.g., from Fig 1’s synthetic RAG), clustering super-voxels to improve IoU (target > 0.75).
- Transformer: A lightweight Transformer (e.g., 2 layers, 4 heads) can process these features, outputting weighted vectors for FCM.
- Evaluation: Compare against your baseline DQN (neuromodulation) and SLIC/FCM (segmentation) using MSE, IoU, and FPS metrics.
Suggested Enhancements
Based on your documents, here are ways to refine and integrate this approach:
- Incorporate RL Tuning (from Neuromodulation)
- Use a DQN (as in your RF paper) to adapt Transformer attention weights or FCM parameters (m, K) dynamically. Reward could be state reconstruction MSE or episodic return, aligning with Fig 3’s 0.05 target.
- Novelty: RL-guided FCM extends Bezdek’s static model to adaptive learning, potentially achieving the 15x return claimed.
- Hybrid with Graph Cuts (from Segmentation)
- Post-process Transformer+FCM clusters with your RAG graph cuts to enforce spatial coherence, as in Fig 1. This combines pre-attention weighting with post-regularization.
- Implementation: Use FCM memberships as unaries in the RAG, refining with normalized cuts (λ=0.5), targeting IoU gains over Fig 2’s 0.70.
- Autoencoder Pre-Processing
- Add a VAE before the Transformer to denoise RF or multi-spectral data, reducing dimensionality while preserving structure (Bezdek’s high-D challenge). This could enhance MSE improvements (e.g., 6% to 8%).
- Test: Apply to N=2 RF data, comparing reconstruction error against Fig 3’s baseline.
- Multi-Beam Scaling (N>2)
- Extend to N=4 multi-beam RF, using the Transformer to handle increased dimensionality (e.g., {P_i, f_i, ϕi, θ_i}{i=1}^4). Validate with your multi-beam extension’s distributed θ⋆.
- Novelty: Scales Bezdek’s FCM to complex RF scenarios, addressing coupling (ε_{ij} from your multi-beam critique).
- Adversarial Robustness
- Train a GAN alongside Transformer+FCM, where the discriminator enforces cluster coherence against noise (e.g., RF camera noise). This aligns with Bezdek’s noise sensitivity concerns.
- Metric: Measure robustness via IoU drop under 10% noise augmentation.
Integration with Your Papers
- RF Neuromodulation: Replace the linear decoder (MSE 0.05, Fig 3) with Transformer+FCM, using RL to tune attention. Test on multi-beam data to exceed 100 return (Fig 2).
- Super-Voxel Segmentation: Use Transformer+FCM on RGB + depth, followed by graph cuts, aiming for IoU > 0.75 at 50 fps (Fig 2). Validate on real MRI data (e.g., BRATS).
Next Steps
- Validation: Generate figures (e.g., MSE vs. episode, IoU vs. FPS) with error bars, using your synthetic datasets.
- Code: Adapt
fcm.pyandgraph_hooks.pyto include a Transformer layer (e.g., PyTorch’snn.TransformerEncoder). - Publication: Target MICCAI (medical focus) or NeurIPS ML for Health with a 6-page draft, emphasizing multi-modal gains.
This approach is a strong evolution of Bezdek’s FCM—let me know if you’d like a chart config or code snippet to kickstart implementation!